Correlación y causalidad
En un blog sobre ciencia y nutrición como es este no puede faltar el tan manido artículo sobre correlación y causalidad. Realmente me pregunto por qué alguien puede querer volver a escribir sobre este tema. Yo, por si acaso, como veo que la gente sigue escribiendo sobre ello, me voy a unir al carro no sea que me vaya a perder algo.
Existe correlación entre dos sucesos cuando siempre (o casi siempre) suceden uno a continuación del otro. Por el contrario, existe causalidad cuando uno de los sucesos implica irremediablemente que acaezca el otro. Veamos un ejemplo muy revelador:
El texto dice:
En el primer caso es evidente que cualquier persona que respire, tarde o temprano, va a acabar comiendo lechugas por las raíces. Esto es así en el 100% de los casos (correlación perfecta). Sin embargo, la respiración no es la causa de que mueran. En el segundo caso, se hace la suposición contraría y ahí si que hay causalidad: el 100% de la gente que no puede respirar se muere. Y además se muere porque no pudo respirar, luego causalidad.
Es más, si me apretáis, podríamos forzar un poco el caso y, circunscribiéndolo a gente que está buceando como sugiere la segunda imagen, podríamos inventarnos que se salva un 8% de la gente que no respira (porque les salvan, por ejemplo) y entonces tendríamos lo siguiente:
Esto nos muestra que, incluso habiendo causalidad, el porcentaje de correlación puede ser menor que en una correlación sin causalidad. Así que, ¡cuidadín!
Filosóficamente la causalidad es un tema espinoso. Tendemos a pensar que la causalidad existe y gracias a ello podemos funcionar en la vida y elaborar modelos, como por ejemplo la física. Sin embargo, podríamos argumentar que la causalidad no es más que una ilusión y que en realidad las cosas suceden al azar y somos nosotros los que les damos sentido. Esto está fuera del ámbito de este artículo pero ahí lo dejo. Basta pensar que ha habido multitud de filósofos (que suelen ser gente lista) devanándose los sesos con el tema.
Fisiológicamente, el problema es que nuestro cerebro está perfeccionado para buscar patrones repetitivos. ¿Os acordáis de las ilusiones ópticas y lo rápido que los niños "aprenden" que el cerebro les está engañando? Pues ese es un ejemplo de detección de patrones.
Los patrones repetitivos denotan correlación, pero en ningún momento se puede inferir causalidad de ellos. ¿Entonces? Entonces hacemos ciencia y, dada una correlación, elaboramos hipótesis y las ponemos a prueba. Si pasan la prueba, entonces sí podemos decir que hay causalidad.
Por ejemplo, tras ver varios incendios podemos formular la hipótesis de que la gente que se quema se muere (ando escatológico hoy). Para comprobar dicha hipótesis planteamos el siguiente experimento: cogemos a 20 personas y a 10 de ellas elegidas al azar les pegamos fuego y esperamos. Si se mueren esos y los demás no, podemos inferir que el fuego es la causa de su muerte, porque es la única diferencia entre los que sobreviven y los que no. Si pasa otra cosa, es que no hay causalidad.
Aunque se puede aplicar a multitud de ámbitos, la dicotomía entre correlación y causalidad se hace especialmente notable en epidemiología. La epidemiología es la aplicación de métodos estadísticos a poblaciones para detectar problemas de salud, sus posibles soluciones, y elaborar hipótesis sobre sus causas. Fijaos bien que digo elaborar hipótesis, no determinar sus causas. Este el quid de la cuestión.
Tendemos a pensar, cuando sale un estudio, que hay causalidad, cuando la mayoria de las veces es correlación. Por ejemplo, cuando nos dicen que el colesterol alto se asocia a enfermedad cardiovascular lo que nos estan diciendo es que hay correlación, no que el colesterol alto cause la enfermedad en si (sí, estás leyendo bien, aquí te lo explican mejor).
Esto tiene muchas implicaciones, entre otras que algunos de los medicamentos que bajan el colesterol no tienen efecto totalmente demostrado sobre el riesgo cardiovascular: simplemente bajan el colesterol (un ejemplo de esto son los fibratos) sin alterar el riesgo cardiovascular. Esto solo puede suceder porque el colesterol no es la causa real, sino una variable que predice la enfermedad cardiovascular pero sin causarla directamente.
Para estar seguros de la causalidad los científicos diseñan estudios de intervención, con metodología similar a la quema de personas que yo propongo más arriba. Por ejemplo, en medicina, se prueba a administrar un medicamento a un subgrupo de personas mientras al otro subgrupo se le da un placebo (una sustancia sin ningún efecto). Si las que recibieron la medicina se curan y las otras no, entonces deducimos que la medicina ha hecho efecto.
A veces esto no se puede hacer por motivos éticos, de presupuesto, técnicos, etc... En esos casos se suele recurrir a estudiar como funciona el mecanismo de correlación/causalidad más a fondo. O se hacen pruebas indirectas, como comprobar la relación entre dosis y respuesta: si, por ejemplo, vemos que fumar está correlacionado con cancer de pulmón y vemos que, cuanto más se fuma, mas probable es el cáncer, eso nos da una pista de que puede haber causalidad.
Como he dicho antes, habrá miles de artículos sobre este tema, tratado hasta la saciedad. Yo solo quería aportar mi vision personal por si a alguien le aclara las cosas.
Os dejo con una tira de xkcd:
Traducción, para los que no sepáis inglés:
Y con una web donde podéis encontrar correlaciones sin causalidad para dar y tomar. A ver quien encuentra la más absurda.
Hale, que no os pase lo que al del cómic... ;-)
Correlación y causalidad
Existe correlación entre dos sucesos cuando siempre (o casi siempre) suceden uno a continuación del otro. Por el contrario, existe causalidad cuando uno de los sucesos implica irremediablemente que acaezca el otro. Veamos un ejemplo muy revelador:
 |
| Origen: http://www.asandiford.com/comic/correlation-causation/ |
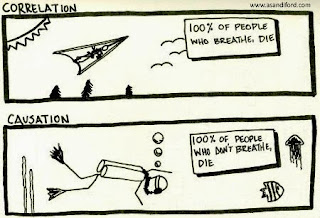
El texto dice:
- Correlación: 100% de la gente que respira muere.
- Causalidad: 100% de la gente que NO respira muere.
En el primer caso es evidente que cualquier persona que respire, tarde o temprano, va a acabar comiendo lechugas por las raíces. Esto es así en el 100% de los casos (correlación perfecta). Sin embargo, la respiración no es la causa de que mueran. En el segundo caso, se hace la suposición contraría y ahí si que hay causalidad: el 100% de la gente que no puede respirar se muere. Y además se muere porque no pudo respirar, luego causalidad.
Es más, si me apretáis, podríamos forzar un poco el caso y, circunscribiéndolo a gente que está buceando como sugiere la segunda imagen, podríamos inventarnos que se salva un 8% de la gente que no respira (porque les salvan, por ejemplo) y entonces tendríamos lo siguiente:
- Correlación: 100% de la gente que respira muere (en el contexto del buceo).
- Causalidad: 92% de la gente que NO respira muere (en el contexto del buceo).
Esto nos muestra que, incluso habiendo causalidad, el porcentaje de correlación puede ser menor que en una correlación sin causalidad. Así que, ¡cuidadín!
Por qué confundimos correlación con causalidad
Filosóficamente la causalidad es un tema espinoso. Tendemos a pensar que la causalidad existe y gracias a ello podemos funcionar en la vida y elaborar modelos, como por ejemplo la física. Sin embargo, podríamos argumentar que la causalidad no es más que una ilusión y que en realidad las cosas suceden al azar y somos nosotros los que les damos sentido. Esto está fuera del ámbito de este artículo pero ahí lo dejo. Basta pensar que ha habido multitud de filósofos (que suelen ser gente lista) devanándose los sesos con el tema.
Fisiológicamente, el problema es que nuestro cerebro está perfeccionado para buscar patrones repetitivos. ¿Os acordáis de las ilusiones ópticas y lo rápido que los niños "aprenden" que el cerebro les está engañando? Pues ese es un ejemplo de detección de patrones.
Los patrones repetitivos denotan correlación, pero en ningún momento se puede inferir causalidad de ellos. ¿Entonces? Entonces hacemos ciencia y, dada una correlación, elaboramos hipótesis y las ponemos a prueba. Si pasan la prueba, entonces sí podemos decir que hay causalidad.
Por ejemplo, tras ver varios incendios podemos formular la hipótesis de que la gente que se quema se muere (ando escatológico hoy). Para comprobar dicha hipótesis planteamos el siguiente experimento: cogemos a 20 personas y a 10 de ellas elegidas al azar les pegamos fuego y esperamos. Si se mueren esos y los demás no, podemos inferir que el fuego es la causa de su muerte, porque es la única diferencia entre los que sobreviven y los que no. Si pasa otra cosa, es que no hay causalidad.
Advertencia
¡no hagáis este experimento en casa!
Gracias
Epidemiología
Aunque se puede aplicar a multitud de ámbitos, la dicotomía entre correlación y causalidad se hace especialmente notable en epidemiología. La epidemiología es la aplicación de métodos estadísticos a poblaciones para detectar problemas de salud, sus posibles soluciones, y elaborar hipótesis sobre sus causas. Fijaos bien que digo elaborar hipótesis, no determinar sus causas. Este el quid de la cuestión.
Tendemos a pensar, cuando sale un estudio, que hay causalidad, cuando la mayoria de las veces es correlación. Por ejemplo, cuando nos dicen que el colesterol alto se asocia a enfermedad cardiovascular lo que nos estan diciendo es que hay correlación, no que el colesterol alto cause la enfermedad en si (sí, estás leyendo bien, aquí te lo explican mejor).
Esto tiene muchas implicaciones, entre otras que algunos de los medicamentos que bajan el colesterol no tienen efecto totalmente demostrado sobre el riesgo cardiovascular: simplemente bajan el colesterol (un ejemplo de esto son los fibratos) sin alterar el riesgo cardiovascular. Esto solo puede suceder porque el colesterol no es la causa real, sino una variable que predice la enfermedad cardiovascular pero sin causarla directamente.
Para estar seguros de la causalidad los científicos diseñan estudios de intervención, con metodología similar a la quema de personas que yo propongo más arriba. Por ejemplo, en medicina, se prueba a administrar un medicamento a un subgrupo de personas mientras al otro subgrupo se le da un placebo (una sustancia sin ningún efecto). Si las que recibieron la medicina se curan y las otras no, entonces deducimos que la medicina ha hecho efecto.
A veces esto no se puede hacer por motivos éticos, de presupuesto, técnicos, etc... En esos casos se suele recurrir a estudiar como funciona el mecanismo de correlación/causalidad más a fondo. O se hacen pruebas indirectas, como comprobar la relación entre dosis y respuesta: si, por ejemplo, vemos que fumar está correlacionado con cancer de pulmón y vemos que, cuanto más se fuma, mas probable es el cáncer, eso nos da una pista de que puede haber causalidad.
Para terminar
Como he dicho antes, habrá miles de artículos sobre este tema, tratado hasta la saciedad. Yo solo quería aportar mi vision personal por si a alguien le aclara las cosas.
Os dejo con una tira de xkcd:
 |
| Origen: https://xkcd.com/552/ |
Traducción, para los que no sepáis inglés:
- Solía pensar que correlación implicaba causalidad.
- Entonces fui a clases de estadística y ahora no lo pienso.
- Parece que las clases ayudaron.
- Bueno, es posible.
Y con una web donde podéis encontrar correlaciones sin causalidad para dar y tomar. A ver quien encuentra la más absurda.
Hale, que no os pase lo que al del cómic... ;-)


Comentarios
Publicar un comentario